Βασικές γνώσεις για τις πιθανότητες

Περί το 1654 ο Blaise Pascal ξεκίνησε να ερευνά τις πιθανότητες για τις ρίψεις στα ζάρια ενώ μαζί με τον Pierre de Fermat θεωρούνται οι θεμελιωτές της θεωρίας των πιθανοτήτων.

Αν και η ανάλυση και εμβάθυνση στους νόμους που διέπουν το πεδίο της μαθηματικής επιστήμης των πιθανοτήτων δεν αποτελεί σκοπό του παρόντος βιβλίου, στην παράγραφο αυτή κρίναμε σκόπιμο να αναφέρουμε ορισμένα πολύ βασικά και χρήσιμα στοιχεία που αφορούν την έννοια των πιθανοτήτων, και τα οποία ωφέλιμο είναι να έχει υπόψη του ο αναγνώστης.

Η πιθανότητα (probability) για να συμβεί ένα γεγονός μπορεί να εκφραστεί είτε ως κλάσμα, είτε ως επί τοις εκατό ποσοστό, είτε ως δεκαδικός αριθμός με τιμές μεταξύ 0 έως 1. Πιθανότητα 0 ή 0% σημαίνει ότι το γεγονός δεν πρόκειται ποτέ να συμβεί. Πιθανότητα 1 ή 100% σημαίνει ότι το γεγονός είναι βέβαιο ότι θα συμβεί. Πιθανότητα 1/4 ή 0,25 σημαίνει ότι κατά μέσο όρο το γεγονός θα συμβεί 1 στις 4 φορές, που συνεπάγεται ότι έχουμε 25% ποσοστό επιτυχίας για να συμβεί το γεγονός και ποσοστό 75% ότι δεν θα συμβεί κ.ο.κ.

Η πιθανότητα να συμβεί ένα γεγονός είναι πάντοτε ένα μείον την πιθανότητα να μην συμβεί το γεγονός αυτό.

Σε κάθε ζήτημα πιθανότητας είναι πολύ σημαντικό να είμαστε σε θέση να προσδιορίζουμε τον αριθμό των γεγονότων και των συνδεόμενων αποτελεσμάτων.

Σε κάθε τυχερό παιχνίδι υπάρχουν οι ευνοϊκές περιπτώσεις, δηλαδή ο αριθμός των αποτελεσμάτων για να κερδίσει ο παίκτης, και οι δυσμενείς περιπτώσεις δηλαδή ο αριθμός των αποτελεσμάτων για να χάσει ο παίκτης.

Το άθροισμα των ευνοϊκών και των δυσμενών περιπτώσεων είναι πάντοτε ίσο με το συνολικό αριθμό των δυνατών αποτελεσμάτων.

Τα παραπάνω θα γίνουν πιστεύουμε πλήρως κατανοητά με τα επόμενα παραδείγματα. Στα παραδείγματα αυτά θα υπολογίσουμε την πιθανότητα να συμβεί ένα γεγονός όταν όλα τα αποτελέσματα είναι εξίσου πιθανά.*

(α) Ας εκτιμήσουμε την πιθανότητα να έρθει “γράμματα” σε μια ρίψη ενός νομίσματος. Επειδή υπάρχουν δύο εξίσου πιθανά αποτελέσματα, δηλαδή “κεφαλή” ή “γράμματα” και επειδή το ευνοϊκό αποτέλεσμα είναι ένα από αυτά, το να έρθει “γράμματα”, συμπεραίνουμε ότι η πιθανότητα να έρθει “γράμματα” σε μια ρίψη είναι ½ ή 0,5 ή 50%.

(β) Έστω ότι έχουμε μέσα σε ένα κουτί 4 κόκκινους και 6 μπλε βώλους, και θέλουμε να βρούμε την πιθανότητα να τραβήξουμε τυχαία με την πρώτη φορά ένα κόκκινο βώλο. Στην περίπτωση αυτή επειδή όλα τα αποτελέσματα είναι εξίσου πιθανά η σχέση που θα χρησιμοποιήσουμε είναι:

(1) Πιθανότητα =

γιατί το ευνοϊκό αποτέλεσμα είναι να τραβήξουμε έναν από τους τέσσερις κόκκινους βώλους, ενώ το σύνολο των δυνατών αποτελεσμάτων είναι και οι δέκα βώλοι μέσα στο κουτί, επειδή είναι εξίσου πιθανό να τραβήξουμε οποιονδήποτε από αυτούς. Έτσι, τελικά η πιθανότητα είναι 0.4, ή, εκφραζόμενη ως ποσοστό επί τοις εκατό, 40%.

(γ) Ας υποθέσουμε ότι έχουμε ένα ζάρι και θέλουμε να φέρουμε το 5 με την πρώτη ζαριά. Όπως γνωρίζουμε ένα ζάρι έχει έξι έδρες που καθεμιά είναι αριθμημένη αντίστοιχα από το 1 έως το 6. Αυτό σημαίνει ότι το σύνολο των δυνατών αποτελεσμάτων είναι 6. Με το ίδιο σκεπτικό όπως και στο προηγούμενο παράδειγμα ισχύει

(δ) Στο παιχνίδι Ρουλέτα ο τροχός αποτελείται από 37 νούμερα. Αυτό σημαίνει ότι ο συνολικός αριθμός των δυνατών αποτελεσμάτων είναι 37. Εάν στοιχηματίσουμε σε ένα νούμερο στην αμέσως επόμενη ρίψη της μπίλιας, έχουμε 1 ευνοϊκή και 36 δυσμενείς πιθανότητες στο σύνολο των 37 δυνατών αποτελεσμάτων και εύκολα προκύπτει ότι η πιθανότητα να έρθει το νούμερο που στοιχηματίσαμε στην αμέσως επόμενη ρίψη της μπίλιας είναι 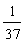δηλαδή 2,7%.

Όσον αφορά τις σύνθετες πιθανότητες εάν το ένα γεγονός είναι ανεξάρτητο από το άλλο πολλαπλασιάζουμε τις απλές πιθανότητες μεταξύ τους για να βρούμε τον συνολικό αριθμό των δυνατών αποτελεσμάτων. Έτσι, για παράδειγμα, ρίχνοντας ένα ζάρι έχουμε όπως γνωρίσαμε 6 δυνατά αποτελέσματα, ενώ ρίχνοντας δύο ζάρια έχουμε 6 Χ 6 = 36 δυνατά αποτελέσματα, όπως φαίνεται και από τον ακόλουθο πίνακα 3-1.

Με τον ίδιο τρόπο όπως προηγουμένως, υπολογίζουμε την πιθανότητα του κάθε αποτελέσματος για το παράδειγμά μας, όπως προκύπτει και από τον παρακάτω πίνακα 3-2.

Πηγές

paignio.com