Καρτεσιανό επίπεδο. Μέτρηση απόστασης

Το καρτεσιανό σύστημα συντεταγμένων είναι ένα ορθογώνιο σύστημα συντεταγμένων που χρησιμοποιείται για να προσδιορίσει ένα σημείο στο επίπεδο ή στο χώρο. Οφείλει το όνομά του στον Καρτέσιο (Descartes) που το εισήγαγε.

Καρτεσιανές συντεταγμένες στο επίπεδο

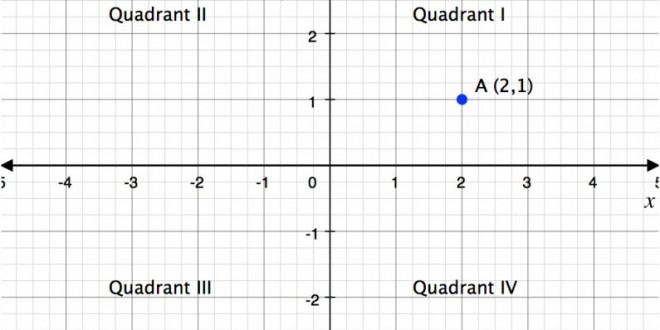
Το καρτεσιανό σύστημα συντεταγμένων στο επίπεδο αποτελείται από δύο προσανατολισμένες ευθείες, κάθετες μεταξύ τους, οι οποίες καλούνται συμβατικά άξονας τετμημένων (οριζόντιος άξονας) και άξονας τεταγμένων (κατακόρυφος άξονας) και συμβολίζονται αντίστοιχα με x και y. Το σημείο όπου τέμνονται λέγεται αρχή του συστήματος συντεταγμένων.

Ένα σημείο πάνω στο καρτεσιανό επίπεδο προσδιορίζεται μοναδικά από ένα ζεύγος αριθμών, την τετμημένη και την τεταγμένη. Η τετμημένη είναι η απόσταση του σημείου από τον άξονα y και η τεταγμένη είναι η απόσταση του σημείου από τον άξονα x. Η τετμημένη και η τεταγμένη αποτελούν τις συντεταγμένες του σημείου. Με αυτή τη σύμβαση, η αρχή των αξόνων ταυτίζεται με το σημείο (0,0).

Επιπλέον ορίζεται απόσταση ίση με 1, σύμφωνα με την οποία αριθμούνται οι άξονες. Οι συντεταγμένες (xP,yP) ενός σημείου P δηλώνουν τη θέση του P κατά την ορθή προβολή του στους άξονες τετμημένων και τεταγμένων αντίστοιχα.